Understanding Properties of the Laplace Transform using Wolfram Language 🐺
In this blog post I'll be sharing my experience in comprehending the Laplace transform using Mathematica.
When I first used the LaplaceTransform function on Mathematica, I wasn't able to get the transforms of Signals which spread to the negative side of the time domain. Digging into the Wolfram Language, I found out that LaplaceTransform on it was defined for the Unilateral Laplace Transform instead. So to get the transforms of non causal signals I manually defined the Bilateral Laplace Transform as LT (wanted a shorter function name!)
$$\text{LT}(\text{f$\_$},\text{t$\_$},\text{s$\_$})\text{:=}\int_{-\infty }^{\infty } f \exp (-s t) \, dt$$
So, here's the Bilateral Laplace Transform in action! Let's compute the Laplace Transform of $-e^{-a t} u(-t)$ and $e^{-a t} u(t)$
Now everything is set to understand laplace transform properties. I'll be noting the properties in the order as discussed in our lecture EN1060.
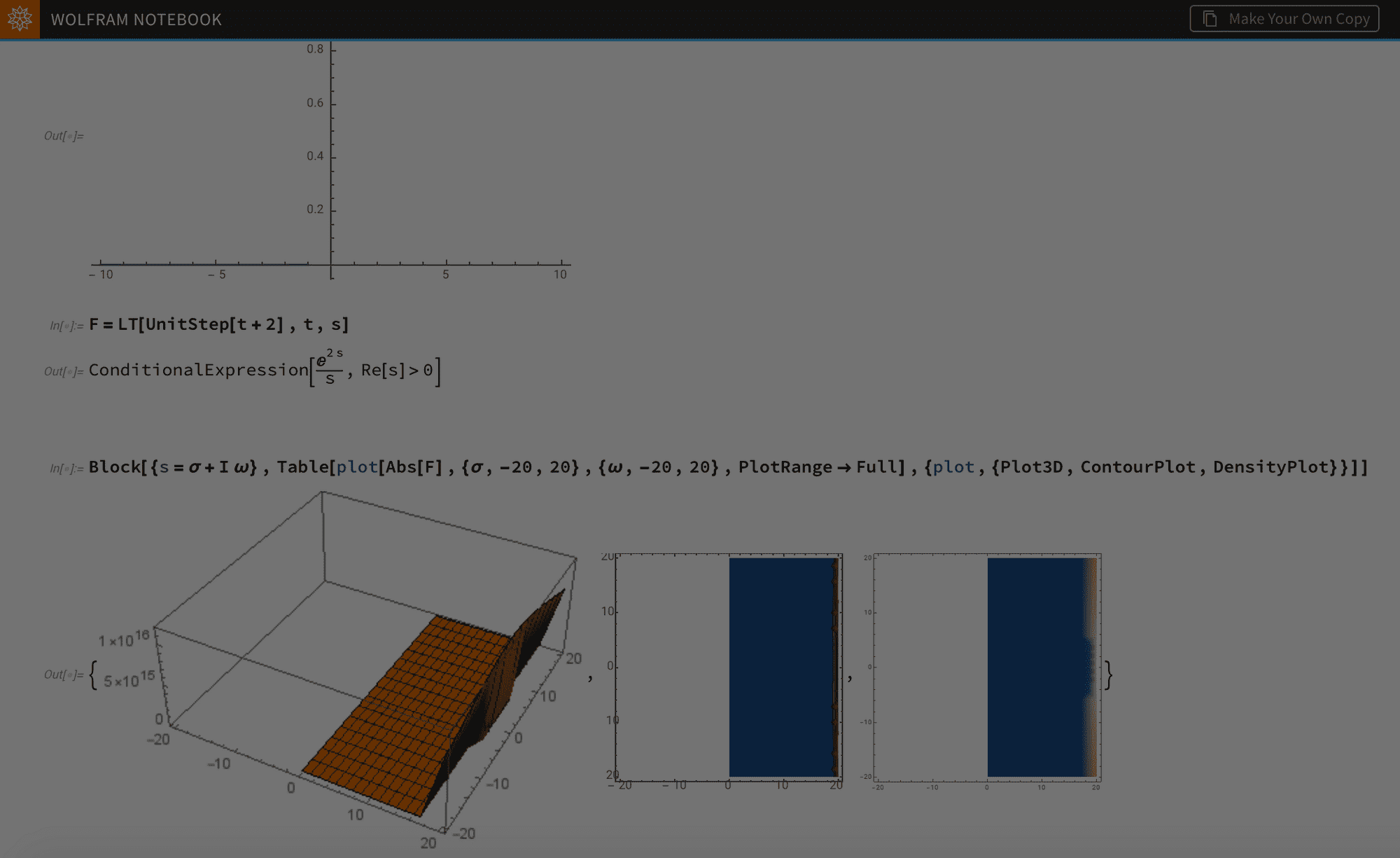
If x(t) is a finite duration signal, then the ROC is the entire s-plane
- If x(t) is a right sided signal, and some $\sigma _0$ such that $\text{Re} {\{s\}}=\sigma _0$ is in ROC, then all values for which $\text{Re} {\{s\}}>\sigma _0$ are in ROC
(simply what this means is in the s-plane, ROC is right sided) so you should get that if the time domain signal is causal, then the ROC will be right sided. See the following code example to see this in action.
(to be updated with examples, and to be extended with Z transform.. Open for suggestions and comments! )
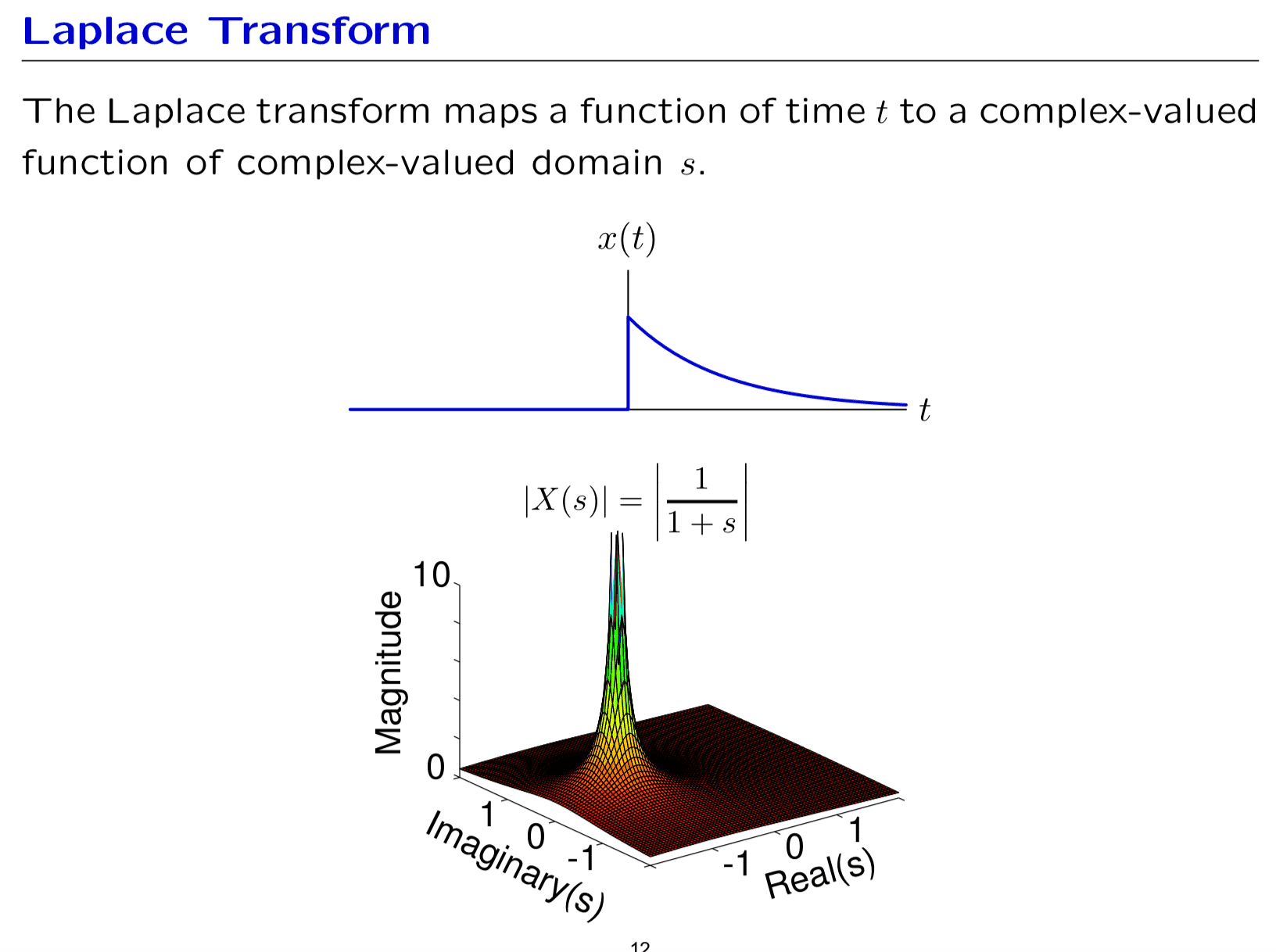
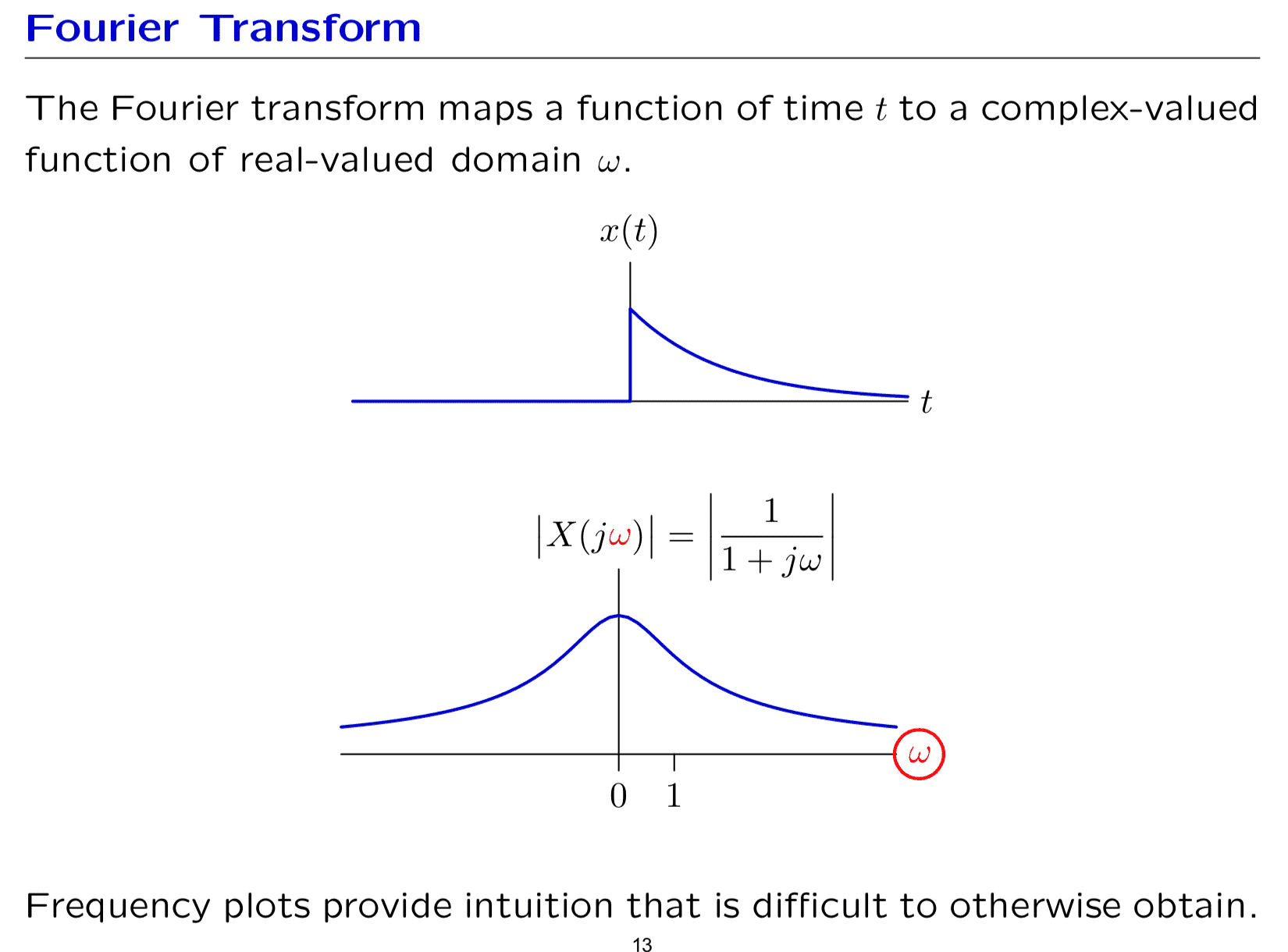
For further reading:
`http://www.ece.uvic.ca/~imanmoaz/teaching_files/Laplace.pdf
`http://www.ee.cityu.edu.hk/~hcso/EE3210_9.pdf
`http://fourier.eng.hmc.edu/e102/lectures/Laplace_Transform/node4.html